So hallo.
Ich bins mal wieder.
Und zwar hab ich mal wieder keinen Plan wie man folgende Sache erstellen könnte und hoffe ihr könnt mir helfen einen Ansatz zu finden:
Ich möchte auf meiner Karte (mit Straßen, Häusern, Gras, Wasser usw.) ein Script einbinden in der der User 2 Punkte anklickt und dann automatisch eine Route berechnet wird - nur über die Straßen (die kürzeste möglichst)
Nur hab ich noch keine Ahnung wie ich sowas um setzen könnte.
Hat da jemand ne Ahnung? Bzw habt ihr überhaupt verstanden was ich will?
Ich bins mal wieder.
Und zwar hab ich mal wieder keinen Plan wie man folgende Sache erstellen könnte und hoffe ihr könnt mir helfen einen Ansatz zu finden:
Ich möchte auf meiner Karte (mit Straßen, Häusern, Gras, Wasser usw.) ein Script einbinden in der der User 2 Punkte anklickt und dann automatisch eine Route berechnet wird - nur über die Straßen (die kürzeste möglichst)
Nur hab ich noch keine Ahnung wie ich sowas um setzen könnte.
Hat da jemand ne Ahnung? Bzw habt ihr überhaupt verstanden was ich will?


 Moderator
Moderator

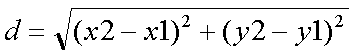

Kommentar